Cost function

Activation function

Cost function is specially designed to measure how bad the network is at classifying the training examples.

A good cost function should be low when the model is right and confident (high), when it’s wrong.

Following are different cost functions.

Log-likelihood cost function

The log-likelihood cost function (also called negative log-likelihood, NLL) is a cost used with a softmax output layer in classification problems.

For one training example with input x and true label y, it is defined as: $C=-\ln a_y^L$ where:

• $a_y^L$ is the network’s output activation (softmax probability) for the correct class y,
• $L$ denotes the output layer

Why its cost function: Function penalizes the model more strongly when it is confident but wrong.

• If the network assigns high probability ($a_y^L\approx 1$) to the correct class, then $-\ln a_y^L$ is close to 0 → low cost.
• If the network assigns low probability ($a_y^L\approx 0$) to the correct class, then $-\ln a_y^L$ becomes very large → high cost

Connection to Cross-Entropy:

• Log-likelihood with softmax is mathematically equivalent to cross-entropy loss with sigmoid for binary classification.
• Gradient simplification: For softmax + log-likelihood, the error term in backpropagation reduces to
  $\boxed{{\delta }_j^L\equiv \frac{\partial C}{\partial z_j^L}=a_j^L-y_j}$ ${\delta }_j^L=a_j^L-y_j$

which is clean and avoids vanishing-gradient issues seen with quadratic cost.

p (true-class probability)	NLL = -log(p)
0.99	0.01005033585350150
0.8	0.2231435513142100
0.5	0.6931471805599450
0.2	1.6094379124341000
0.05	2.995732273553990

---

Quadratic cost

$C=\frac{1}{2}(y-a{)}^2$

---

Cross Entropy cost function

$C=-\frac{1}{n}{\sum }_{i=1}^n[y^{(i)}\log a^{(i)}+(1-y^{(i)}\left)\log \right(1-a^{(i)}\left)\right]$

where $a$ is the neuron’s output, and $y$ is the desired output.

Zero when predictions are correct: If the network’s output matches the desired target (say y=1,a≈1 or y=0,a≈0), the log terms vanish, so the cost tends toward 0. That matches our intuition that “better predictions = smaller cost”. We get low surprise if the output is what we expect, and high surprise if the output is unexpected.

Cross-entropy is positive, and tends toward zero as the neuron gets better at computing the desired output, y, for all training inputs, x. These are both properties we’d intuitively expect for a cost function.

Why log is used in cross entropy function?

If your model says “the probability of class 1 is 0.01” but the truth is class 1, you want a big penalty—because the model was confident and wrong.

So we need a function that:

• Rewards high probability on the correct class.
• Punishes sharply when the correct class is assigned a tiny probability.

The logarithm has two key properties:

• Log squashes probabilities
  • log⁡(1)=0 → perfect prediction = no penalty.
  • log⁡(0.9) is a small negative → almost correct = small penalty.
  • log⁡(0.01) is a big negative → very wrong = huge penalty.
• Log turns products into sums
  • Probabilities of independent events multiply, but logs let us add them.
  • That makes math neat for averaging over many training examples.

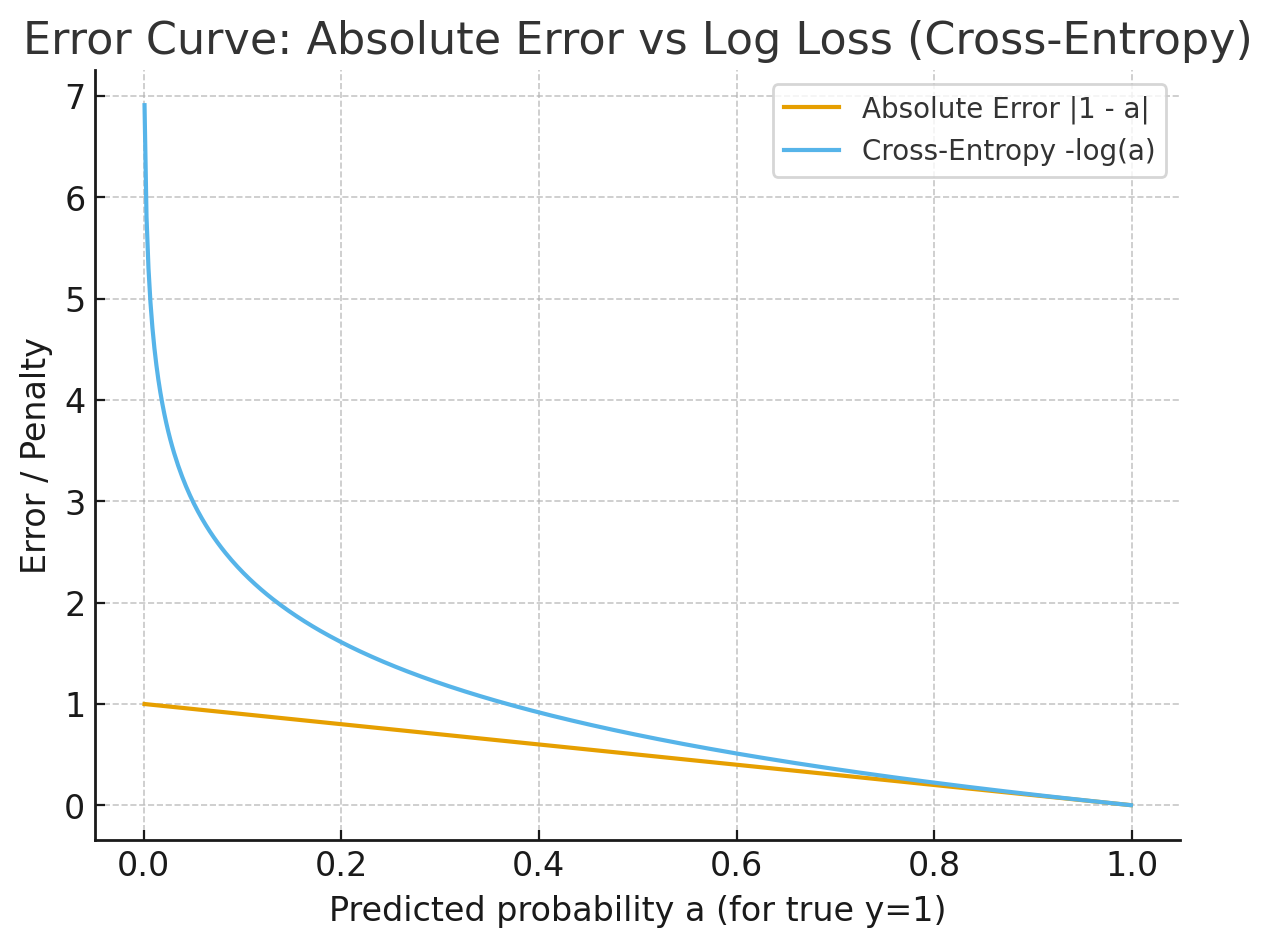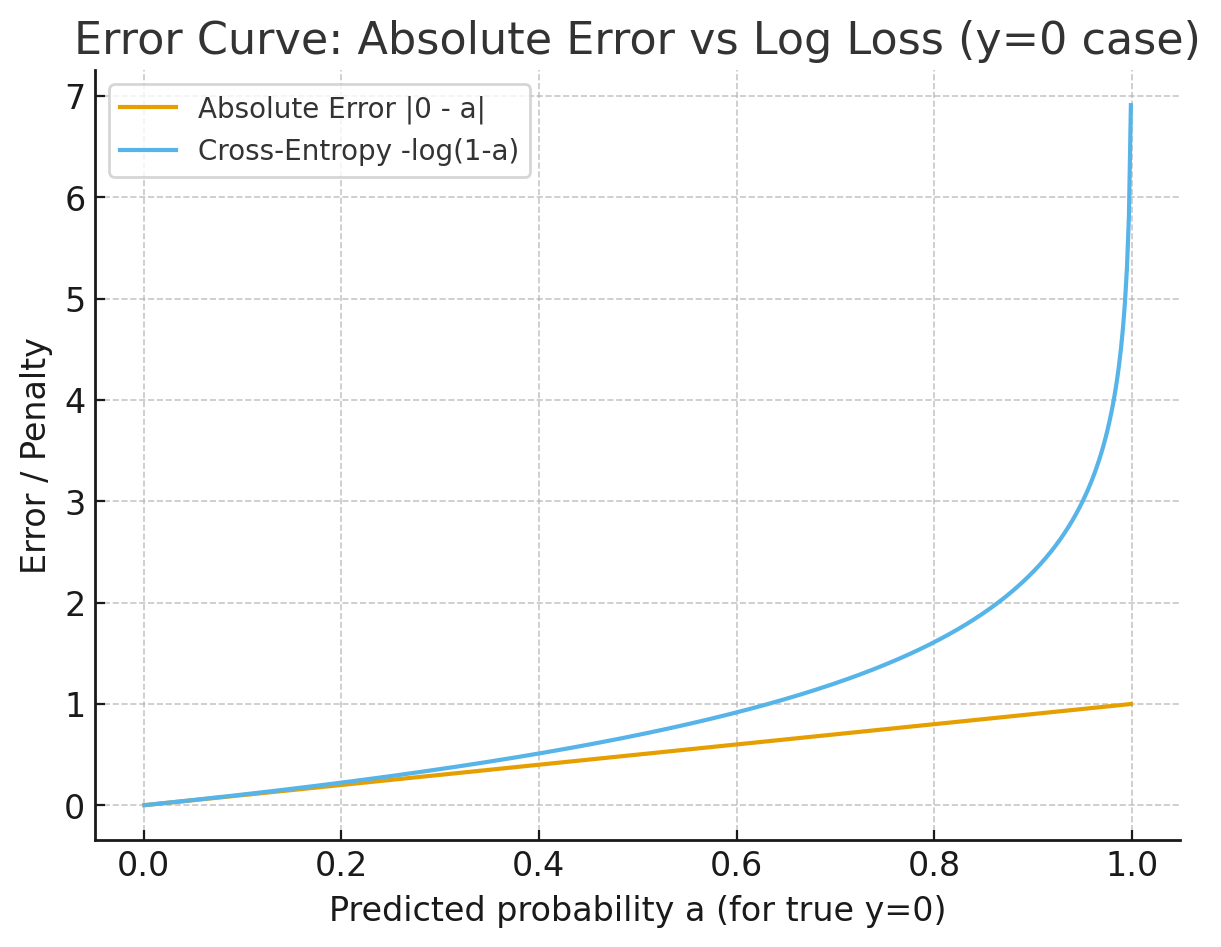That steep “blow up” is exactly why logs are used—it forces the network to really avoid assigning near-zero probability to the correct class.

• The absolute error curve (LHS) is a straight line going gently from 1 → 0 as predictions improve.
• The log error curve (LHS) is flat near 1 (small penalty when correct) but shoots up steeply as predictions get close to 0 (huge penalty when confidently wrong).

How log turns product into sum?

Analogy to the brain

Imagine you bet on outcomes:

• If you’re almost sure but wrong, it hurts a lot.
• If you were uncertain, it hurts less. The log penalty encodes this “confidence-weighted mistake,” forcing the network to not only be correct but confidently correct.

How cost function changes between classification problems, and regression problems?

Classification problems: (dog vs cat, digit 0–9, etc.) How probable if given image is cat or dog? Predictions are probabilities. If the true class has probability $yj=1$, then −log⁡(aj) measures how surprised the model is. The sharper penalty helps the model adjust faster when it’s way off. Typical cost functions is Cross-entropy (with sigmoid or softmax outputs).

Regression problems: Here the outputs are continuous values (price, temperature, torque). Typical cost functions are Mean Squared Error (MSE) or Mean Absolute Error (MAE). Regression = “How far off is your number from the true value?” → distance-based loss (MSE, MAE).

Why not cross-entropy here?
Because outputs aren’t probabilities between 0 and 1, they’re real numbers. Forcing a log probability doesn’t make sense.

When should we use the cross-entropy instead of the quadratic cost?