Overfitting

What is overfitting

Overfitting means the model learns not just the underlying “signal” in the training data, but also the random noise or idiosyncrasies. So it does very well on training data, but fails to generalize to new, unseen data.

• Signal = the true underlying pattern or relationship in the data.
  Think of it as the “law of nature” that actually governs how inputs relate to outputs.
• Noise = random fluctuations, measurement errors, or quirks in the data that don’t reflect the true pattern.

Imagine you’re measuring the height of a person:

• The signal is their true height (say, 175.0 cm).
• The noise is what sneaks in if your measuring tape bends, or the person’s shoes add 1 cm, or you misread by a few millimeters.

If you collect many measurements, the true signal is consistent, but the noise scatters around it.

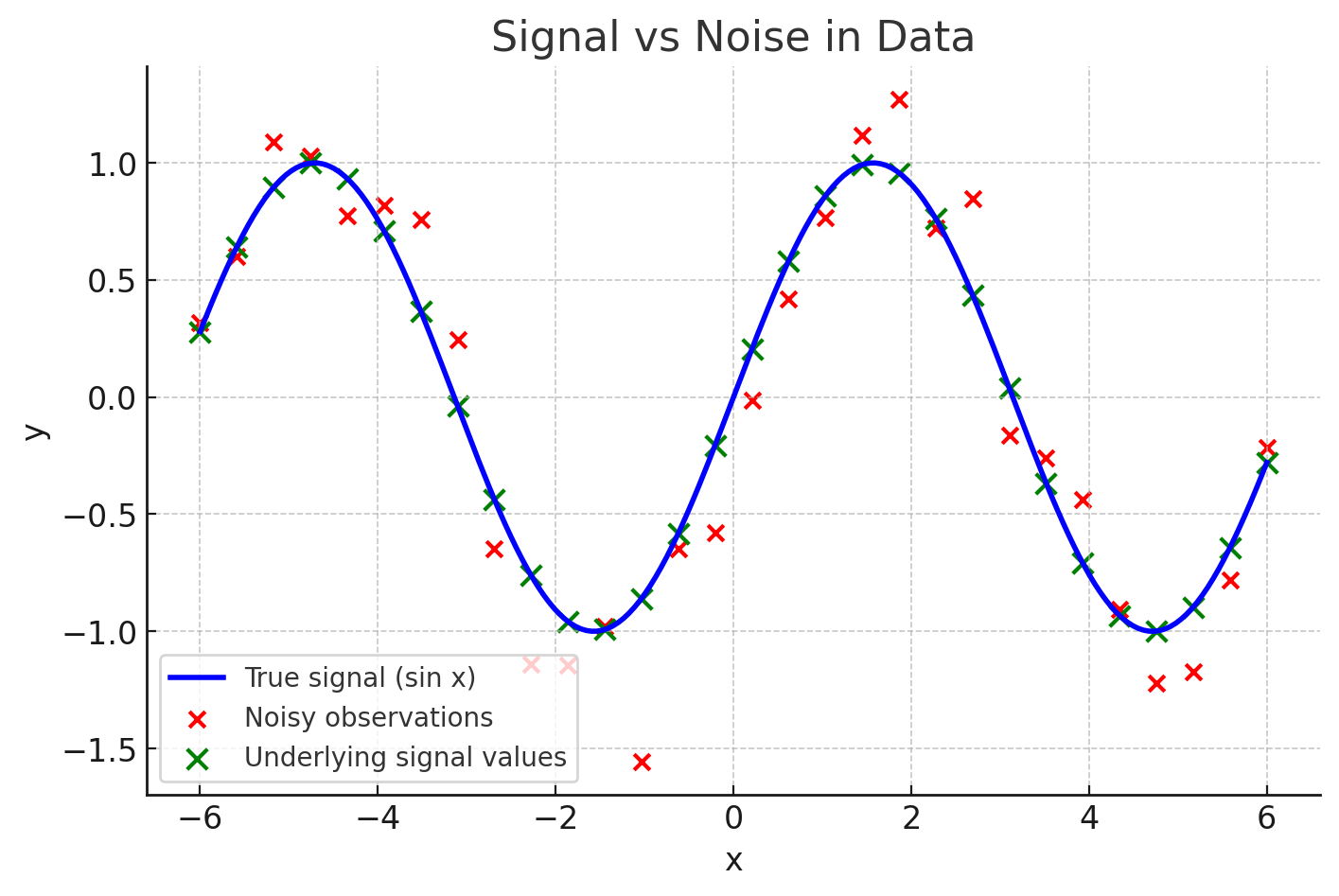
• Blue curve = the signal (the true underlying law, y=sin⁡(x).
• Green X’s = what the signal would be at sampled points, if there were no measurement error.
• Red dots = the noisy observations we actually see after adding random fluctuations.

👉 Overfitting happens when a model tries too hard to chase those red dots — including their random wiggles — instead of capturing the smoother blue curve.

How overfitting captures noise?

How to identify overfitting?

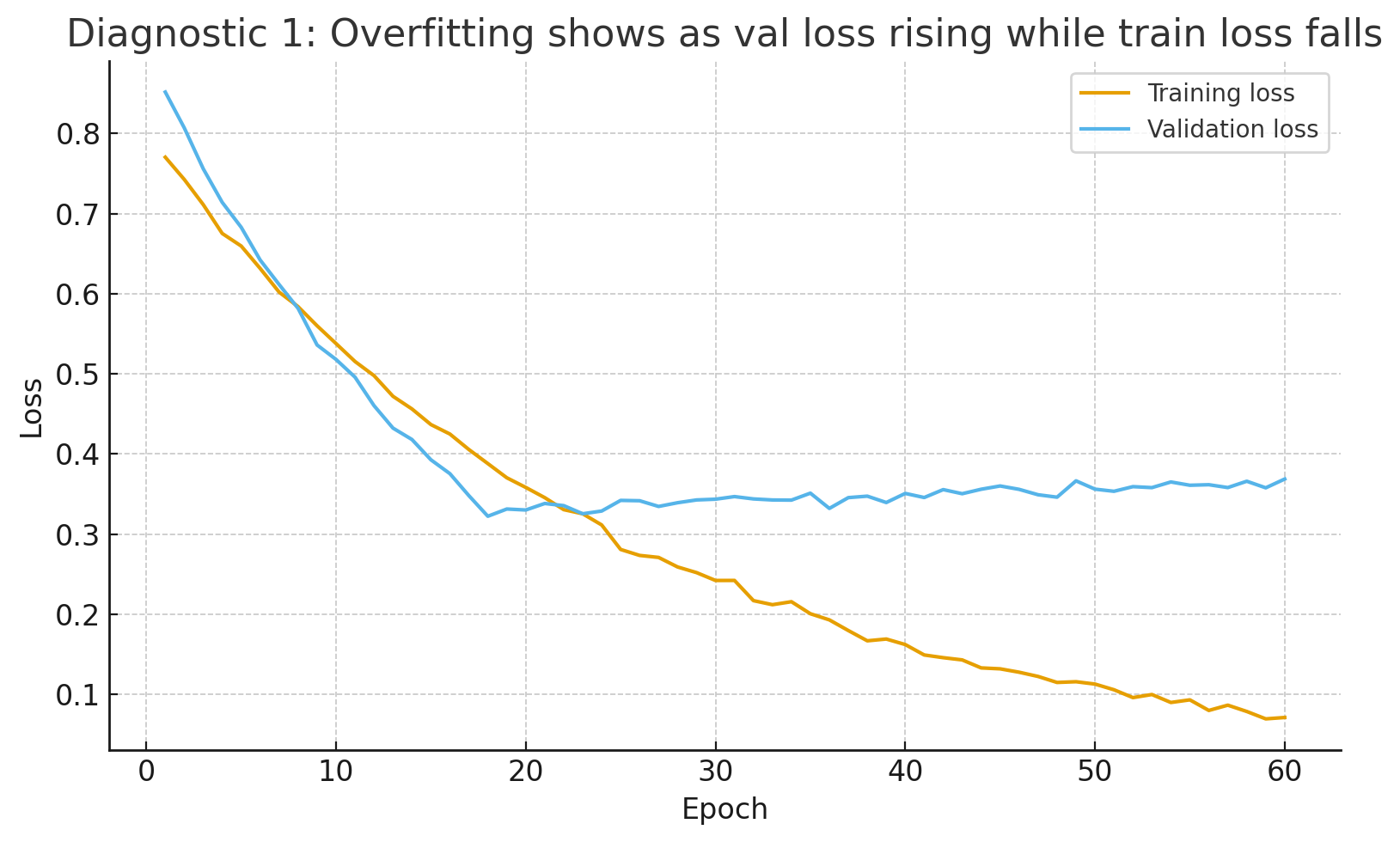
Train vs Val loss (by epochs)
The validation curve bottoms out, then creeps up while training loss keeps falling → classic overfitting onset.

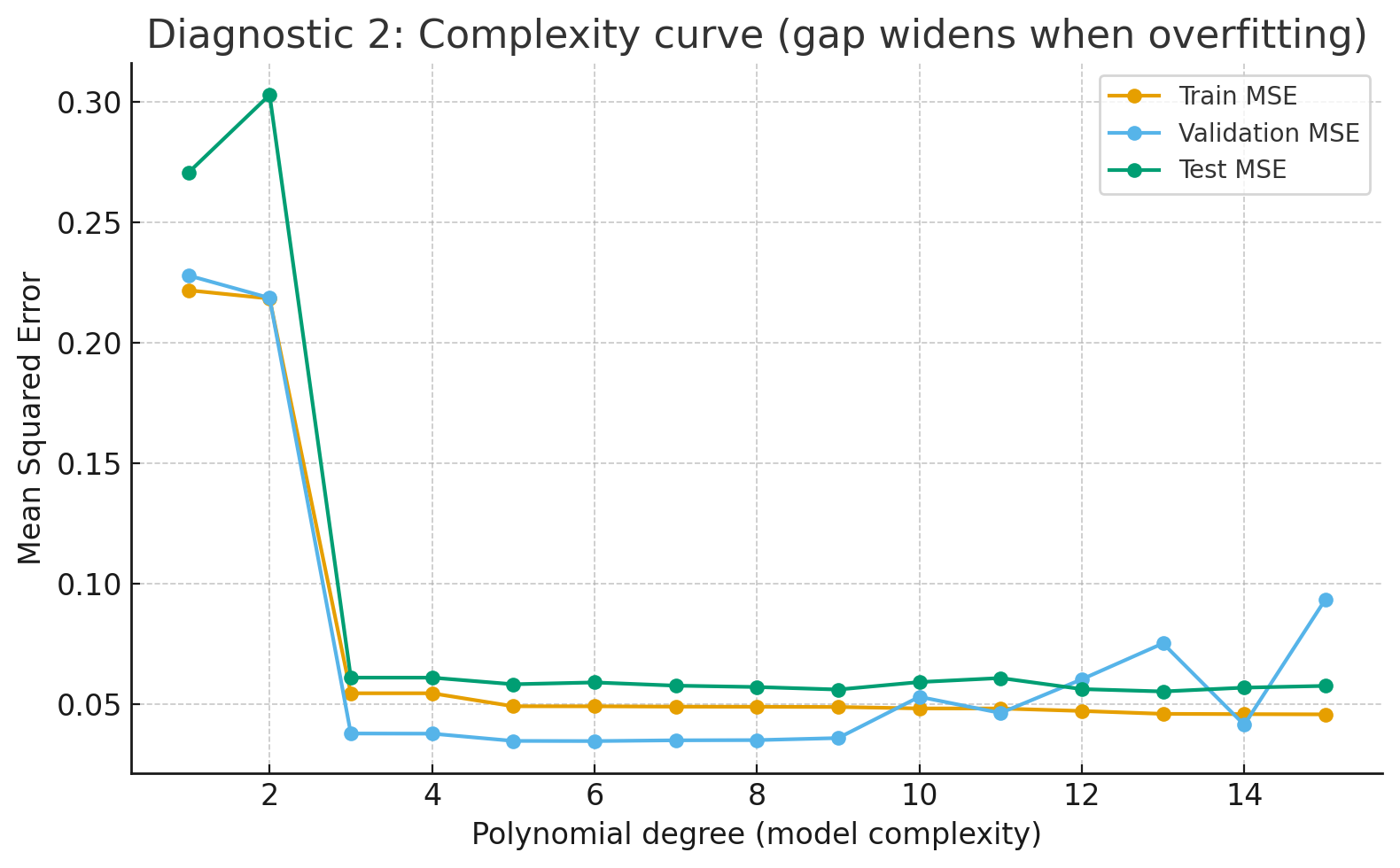
Complexity curve (by model degree)
As degree rises (Complexity of neural network), train MSE keeps dropping, but val/test MSE turn up → model is fitting noise.

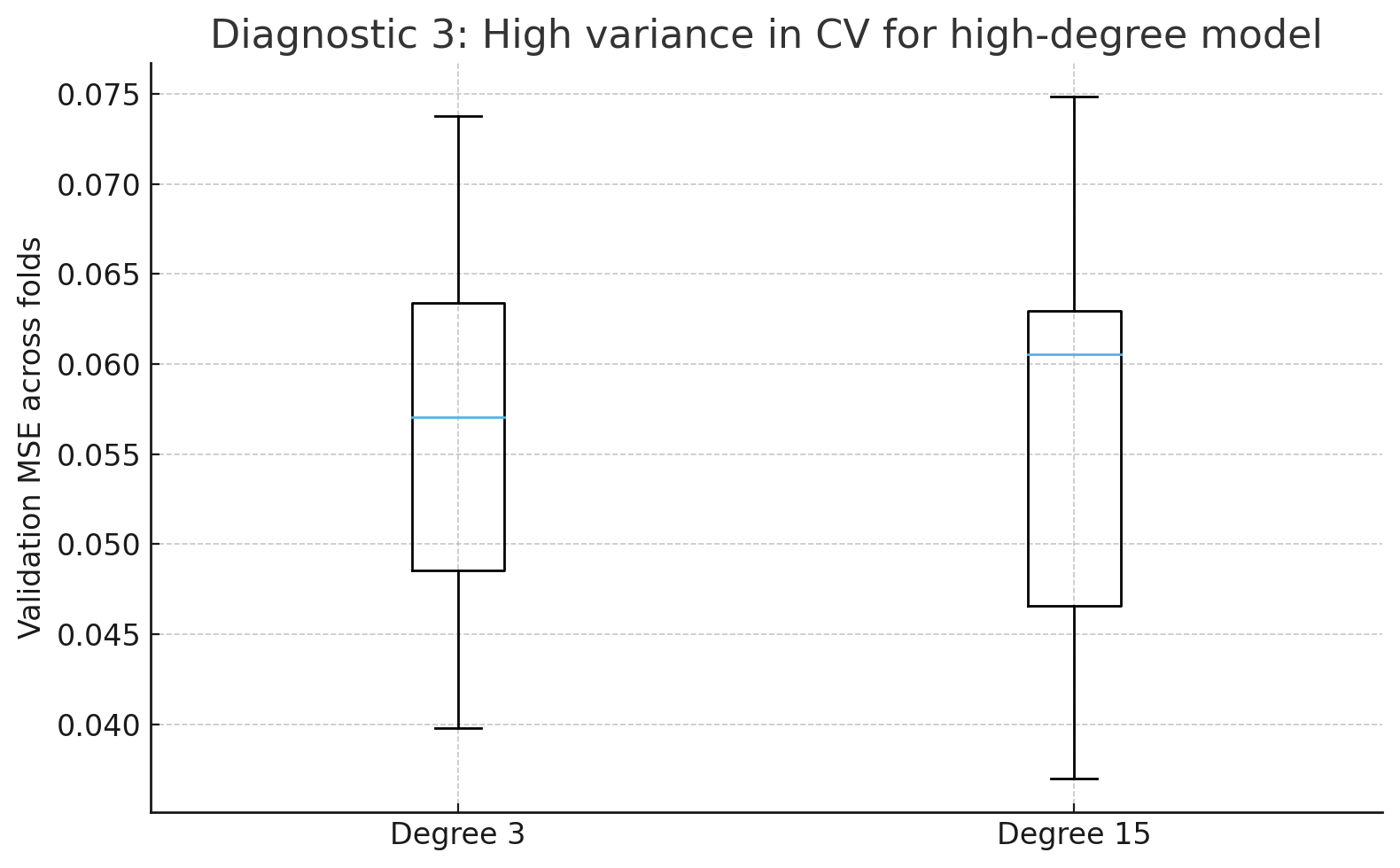
Cross-validation (CV) variance
The boxplot shows higher/less stable fold errors for the high-degree model → high variance behavior.

What cross-validation does

• You split your dataset into several folds.
• Train on some folds, validate on the rest, rotate.
• This gives you multiple validation errors for the same model.

What “variance” means here

• If the model is stable, its validation error should be about the same no matter which folds you trained on.
• If the model is unstable (high variance), then performance jumps around depending on the exact data subset:
  • Sometimes validation error is small.
  • Other times it’s large.

That’s what we saw in the boxplot:

• Degree 3 (simple model): all folds give similar errors → low variance.
• Degree 15 (complex model): fold errors are spread out → high variance.

---

Why use validation_data to prevent overfitting rather than test_data?

Roles of the three data sets

• Training set → used to fit model parameters (weights).
• Validation set → used to tune decisions during training (when to stop, which hyperparameters to pick).
• Test set → used once at the very end to report unbiased performance.

How validation data is actually used inside training?

Training loop without validation

• Epoch 1 → update weights on training set.
• Epoch 2 → update weights on training set.
• … keep going until some fixed number of epochs.
• Risk: you don’t know when overfitting starts.

Training loop with validation Here’s the typical cycle:

1. Forward/backprop on training set → update weights.
2. At the end of each epoch, run the current model on the validation set (no weight updates, just measure error).
3. Record validation loss/accuracy alongside training loss.
4. Use it to make decisions:
   • Early stopping: if validation loss stops improving for N epochs, halt training.
   • Hyperparameter tuning: compare models with different learning rates, depths, or dropout rates on validation scores. Pick the best one.
   • Regularization feedback: if validation loss diverges while training loss falls, you know you need more regularization or data augmentation.

Validation is like a coach watching from the sidelines:

• You (the model) practice on training drills.
• After each drill (epoch), the coach gives feedback on a fresh set (validation).
• The coach decides when you’re peaking — before you get sloppy by memorizing drills.

---

Regularization

Regularization helps reduce overfitting by penalizing complexity, steering the model toward simpler functions that capture the signal, not the noise.

Regularization = any technique that discourages the model from becoming too complex.

Mathematically, we add a penalty to the cost function that makes “too flexible” or “too large” solutions less attractive.

Why do we need it?

• Overfitting happens when the model bends itself to match noise in training data.
• Regularization acts like a “discipline rule”:
  • “Don’t let weights grow too big.”
  • “Don’t rely on one feature too much.”
  • “Don’t memorize every detail.”
• This forces the model to find simpler patterns → better generalization.

Imagine you’re fitting a curve through points:

• Without regularization: the curve can wiggle wildly to hit every point (including noisy outliers).
• With regularization: we say “wiggles cost extra.” The best curve will trade off: it won’t hit every point perfectly, but it’ll stay smoother → closer to the true signal.

Regularization reshapes the cost function:

• Without it → many equally good, wild solutions.
• With it → best solution is the one that’s not only accurate, but also simple (small weights, smooth function).

Common types

1. L2 regularization (Ridge)
   • Add penalty $\lambda \sum wi2$
   • Pushes weights to be small and spread out.
   • Keeps model smooth.