Neural Network Learning Polynomial

Neural network can learn any mathematical function so the polynomial. Polynomial example gives intuitive understanding how complexity in mathematical function increases so the depth or number of neuron in the model.

With enough neurons, a NN can approximate any continuous function on a bounded domain — including polynomials, sine waves, or something crazy like stock prices.

Why polynomials are a good analogy

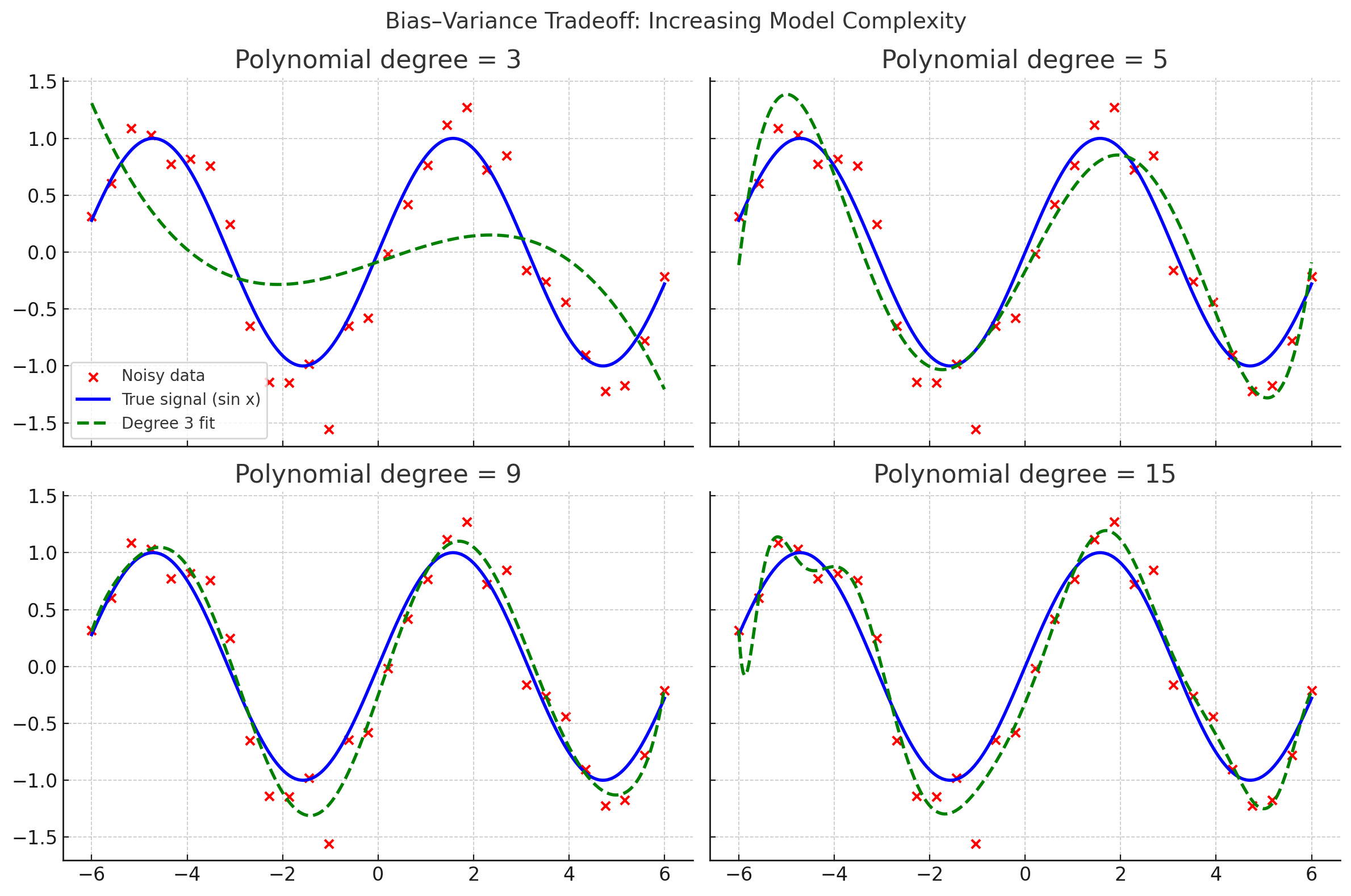
• Polynomial degree = a knob to increase complexity:
  • Degree 1 → only straight lines.
  • Degree 3 → can bend once or twice.
  • Degree 15 → can bend many times (possibly too much). So, higher degree = more expressive model, able to represent more complex shapes.
• Neural networks have knobs too:
  • Depth (layers): allows compositions of functions (more expressive).
  • Width (neurons): more parallel terms/features to combine.
  • Shallow/simple NN = like low-degree polynomial → limited shapes, high bias.
  • Deep/wide NN = like high-degree polynomial → can represent very wiggly/complex patterns, risk of overfitting. So “increasing degree” ≈ “increasing depth/width.” Both raise model capacity.

Intuitive mapping

• Polynomial degree ↑ → more terms, can bend to fit noise.
• NN layers/neurons ↑ → more parameters, can bend to fit noise.

So when we say:

• Degree 3 polynomial underfits = like a very small neural net (too simple).
• Degree 15 polynomial overfits = like a very large neural net trained too long (too complex for data size).

Why does this matter?

• Degree is an easy-to-see slider for model complexity in polynomials.
• Neural network size (parameters) + training epochs act as that slider in deep learning.
• Overfitting risk grows the same way in both worlds.